This blog post is a small excerpt from my work on paper-annotations for the task of question answering. This repo contains a collection of important question-answering papers, implemented from scratch in pytorch with detailed explanation of various concepts/components introduced in the respective papers. The illustrations in this blog post have been created by me using https://www.diagrams.net/. You can find the other references below.

Depthwise Separable Convolutions

Depthwise separable convolutions serve the same purpose as normal convolutions with the only difference being that they are faster because they reduce the number of multiplication operations. This is done by breaking the convolution operation into two parts: depthwise convolution and pointwise convolution.

Depthwise separable convolutions are used rather than traditional ones, as we observe that it is memory efficient and has better generalization.

Let's understand why depthwise convolutions are faster than traditional convolution. Traditional convolution can be visualized as,

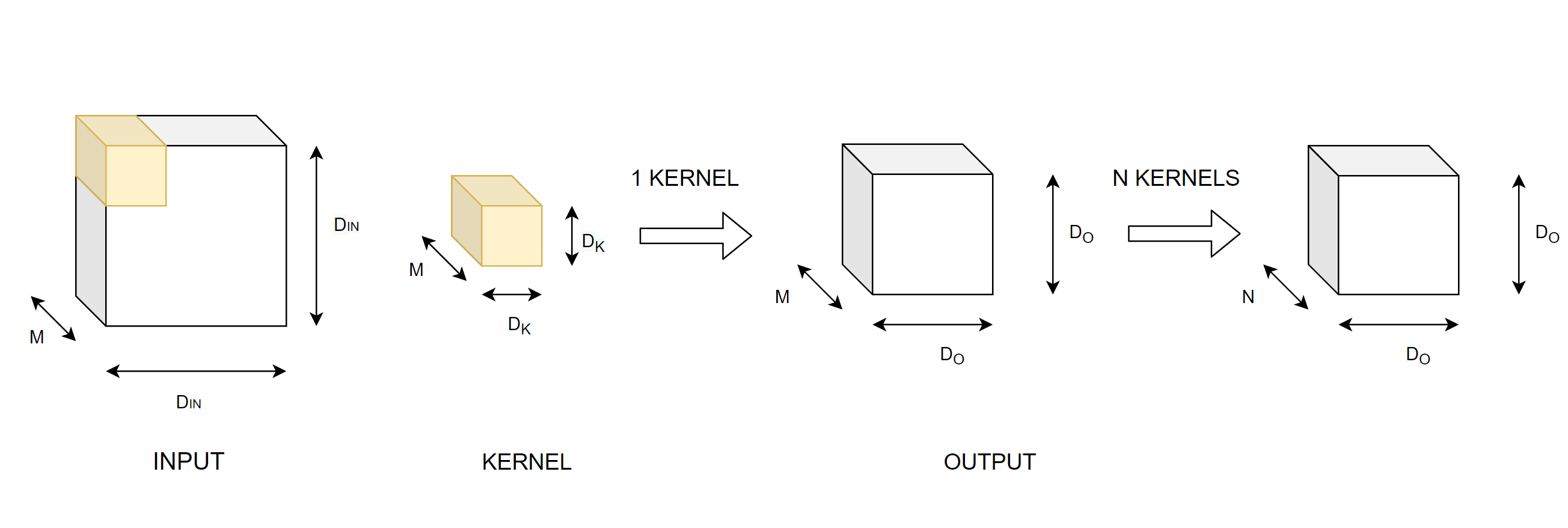
Let's count the number of multiplications in a traditional convolution operation.
The number of multiplications for a single convolution operation is the number of elements inside the kernel. This is $D_{K}$ X $D_{K}$ X $M$ = $D_{K}^{2}$ X $M$. To get the output feature map, we slide or convolve this kernel over the input. Given the output dimensions, we perform $D_{O}$ covolutions along the width and the height of the input image. Therefore, the number of multiplications per kernel are $D_{O}^{2}$ X $D_{K}^{2}$ X $M$.
These calculations are for a single kernel. In convolutional neural networks, we usually use multiple kernels. Each kernel is expected to extract a unique feature from the input. If we use $N$ such filters, then number of multiplications become $N$ X $D_{O}^{2}$ X $D_{K}^{2}$ X $M$.

Depthwise convolution

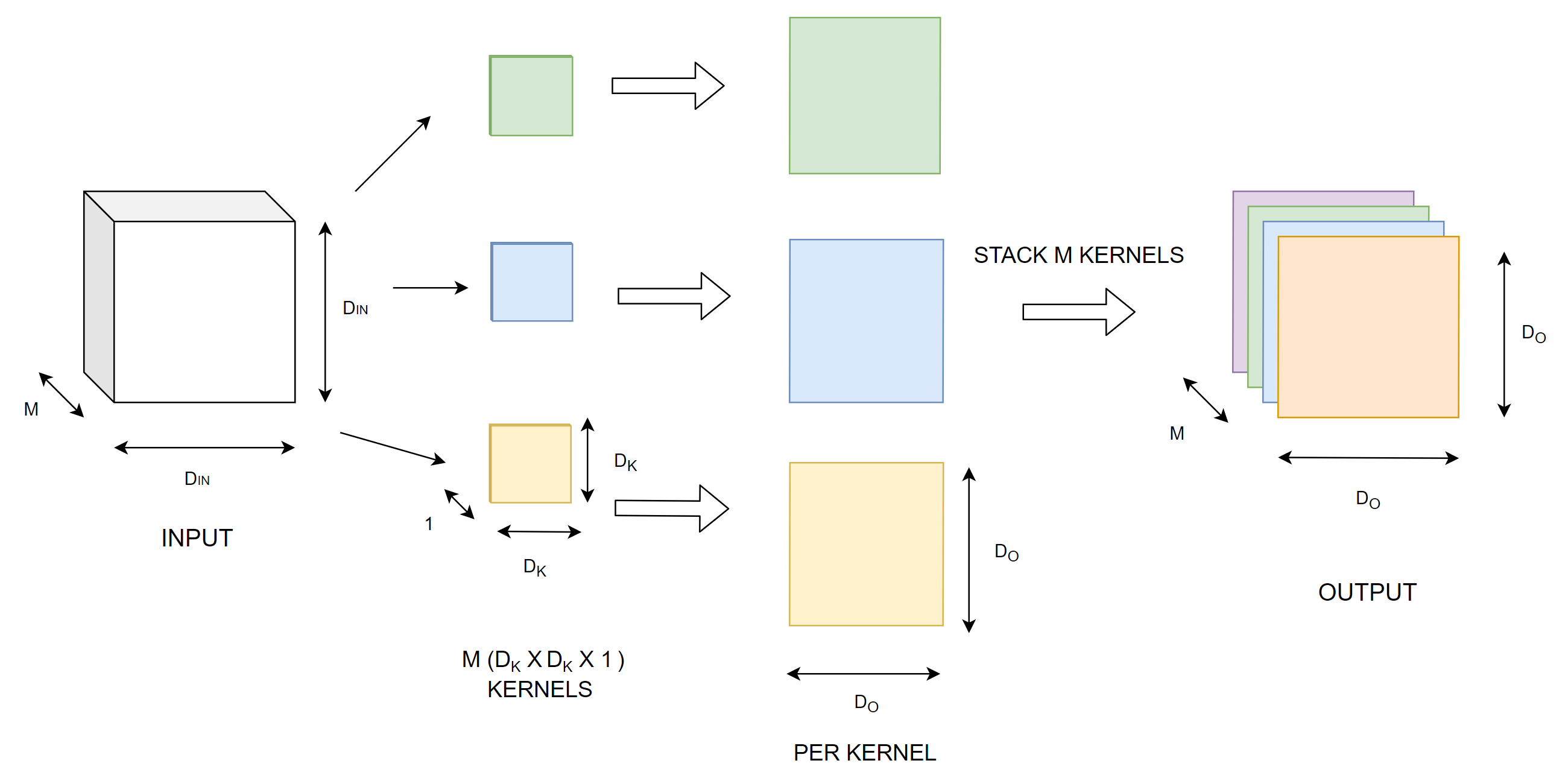
In depthwise convolution we perform convolution using kernels of dimension $D_{K}$ X $D_{K}$ X 1. Therefore the number of multiplications in a single convolution operation would be $D_{K}^{2}$ X $1$. If the output dimension is $D_{O}$, then the number of multiplications per kernel are $D_{K}^{2}$ X $D_{O}^{2}$. If there are $M$ input channels, we need to use $M$ such kernels, one kernel for each input channel to get the all the features. For $M$ kernels, we then get $D_{K}^{2}$ X $D_{O}^{2}$ X $M$ multiplications.

Pointwise convolution

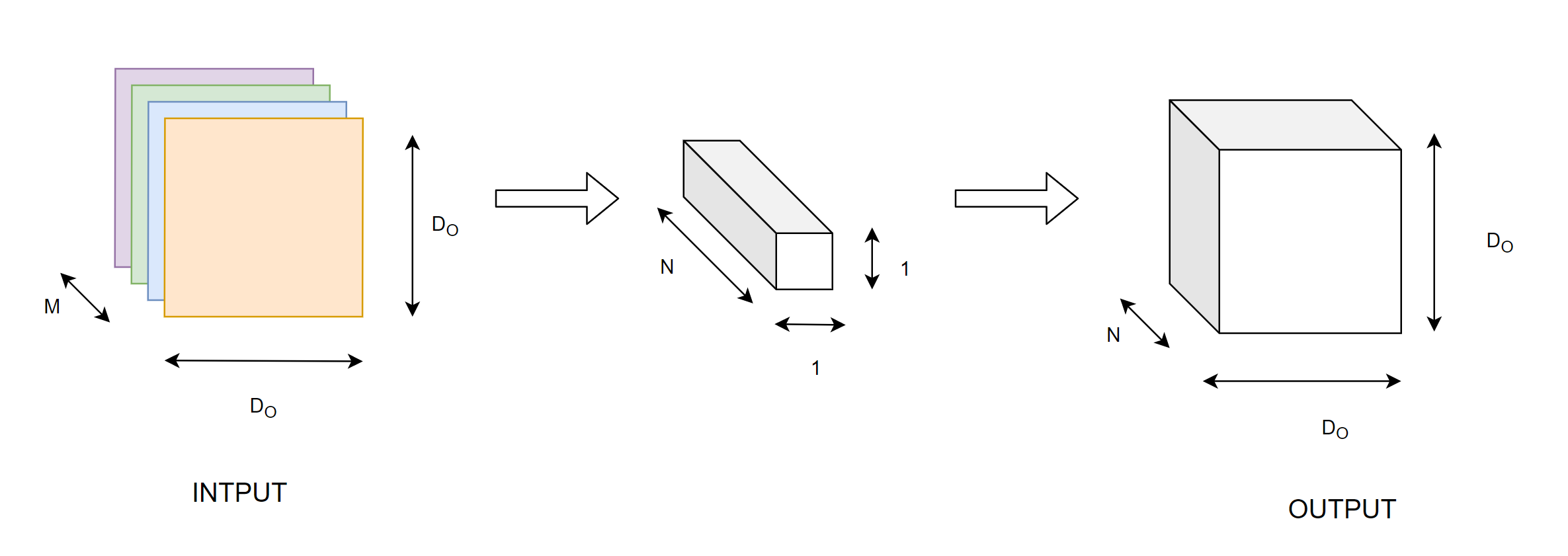
This part takes the output from depthwise convolution and performs convolution operation with a kernel of size 1 X 1 X $N$, where $N$ is the desired number of output features/channels. Here similarly,
Multiplications per 1 convolution operation = 1 X 1 X $M$
Multiplications per kernel = $D_{O}^{2}$ X $M$
For N output features = $N$ X $D_{O}^{2}$ X $M$

Adding up the number of multiplications from both the phases, we get,

$$ =\ N\ .\ D_{O}^{2} \ .\ M \ +\ D_{K}^{2}\ .\ D_{O}^{2}\ .\ M $$ $$ =\ D_{O}^{2}\ .\ M (N + D_{K}^{2}) $$

Comparing this with traditional convolutions,

$$ =\ \frac {D_{O}^{2}\ .\ M\ (N + D_{K}^{2})} {D_{O}^{2}\ .\ M\ .\ D_{K}^{2}\ .\ N}$$

$$ =\ \frac{1}{D_{K}^{2}}\ +\ \frac{1}{N} $$

This clearly shows that the number of computations in depthwise separable convolutions are lesser than traditional ones. In code, the depthwise phase of the convolution is done by assigning groups as in_channels. According to the documentation,

At groups= in_channels, each `nput channel is convolved with its own set of filters, of size:$\left\lfloor\frac{out\_channels}{in\_channels}\right\rfloor$

Implementation

Following is an implementation for the layer discussed above. This is a standalone implementation of the layer and can be plugged into any application/larger model where it is used as a component.

import torch
from torch import nn

class DepthwiseSeparableConvolution(nn.Module):
    
    def __init__(self, in_channels, out_channels, kernel_size):
        
        super().__init__()
      
            
        self.depthwise_conv = nn.Conv2d(in_channels=in_channels, out_channels=in_channels,
                                    kernel_size=kernel_size, groups=in_channels, padding=kernel_size//2)

        self.pointwise_conv = nn.Conv2d(in_channels, out_channels, kernel_size=1, padding=0)

    
    def forward(self, x):
        
        # Interpretations
        # x = [bs, seq_len, emb_dim] for NLP applications
        # x = [C_in, H_in, W_in] for CV applications
        x = self.pointwise_conv(self.depthwise_conv(x))
      
        return x

References